¿Se puede medir la incertidumbre? Una aproximación a Conformal Prediction

La literatura de Heródoto y Cicerón nos ha permitido preservar la historia de Creso, quien fue rey de Lidia. Consultando a un oráculo, Creso recibió una predicción marcada por una trágica ambigüedad: “Si cruzas el río Halys, destruirás un gran imperio”. Convencido de que tal augurio presagiaba la caída del imperio persa, Creso no se percató de la doble interpretación hasta que fue demasiado tarde. Cruzó el río y el imperio que finalmente se derrumbó fue el suyo.

Esta anécdota trae consigo una lección que sigue siendo relevante a pesar del tiempo: las predicciones siempre conllevan cierto grado de incertidumbre, lo que también aplica al ámbito de la inteligencia artificial y del aprendizaje automático.

Depositar nuestra confianza en estos sistemas no debería ser un acto de fe. La confianza debería estar fundamentada en la robustez de los modelos y en una comprensión profunda de que, si bien siempre existirá incertidumbre, esta puede cuantificarse.

La única certeza es la incertidumbre

En el contexto del aprendizaje automático, la incertidumbre puede surgir de múltiples fuentes y afecta a todos los modelos. Puede ser el resultado de datos incompletos, mediciones imprecisas, o simplemente de la variabilidad inherente al fenómeno que estamos tratando de modelar.

Por ello, la capacidad de cuantificar y comunicar la incertidumbre cambia la manera en que interactuamos con la tecnología, permitiéndonos comprender mejor las predicciones, pero también sus límites. Esto, a su vez, fomenta un enfoque más crítico y analítico hacia la toma de decisiones en un mundo cada vez más automatizado y orientado por datos.

Conformal prediction: ¿qué es y cómo funciona?

Si bien la incertidumbre es inevitable, existen técnicas que nos ayudan a manejarla.Una de ellas es conformal prediction, que nos ofrece un nivel de certidumbre parametrizable sobre las predicciones de un modelo.¹ Para entender lo que hace, imaginemos que creamos un modelo de aprendizaje automático con el fin de hacer recomendaciones a nuestros clientes con base en sus intereses en el ámbito de las finanzas.

Para ello, partimos de un problema de clasificación: para que las recomendaciones sean personalizadas, debemos clasificar a los clientes entre “inversores”, “ahorradores”, y demás categorías que puedan servir al modelo para que asocie la recomendación de salud financiera con la persona indicada. Pero, las personas pueden combinar varias categorías, por lo que, al clasificarlos, el modelo podría discernir que pertenecen más a una categoría que a otra. Aquí, la predicción (“esta persona es ahorradora”) se vería como una afirmación taxativa aun cuando parte de un hecho incierto.

En cambio, cuando aplicamos conformal prediction, la predicción trae consigo un conjunto de posibles resultados, cada uno con sus respectivos niveles de confianza.²

En un caso donde un cliente posea características afines a dos categorías, el modelo nos dirá que puede pertenecer a ambas, y no lo asociará rotundamente con una de ellas. Así, nos estaríamos equipando con mucho más conocimiento que si nos quedamos únicamente con la clase que contenga la probabilidad más alta.

En nuestro caso, tenemos un cliente que podría ajustarse a un perfil ahorrador y también a un perfil de control de gasto. Ambas categorías podrían ser correctas, cada una con un nivel de confianza determinado. Sin embargo, la probabilidad de que el cliente se ajuste al perfil de deuda es sustancialmente menor.

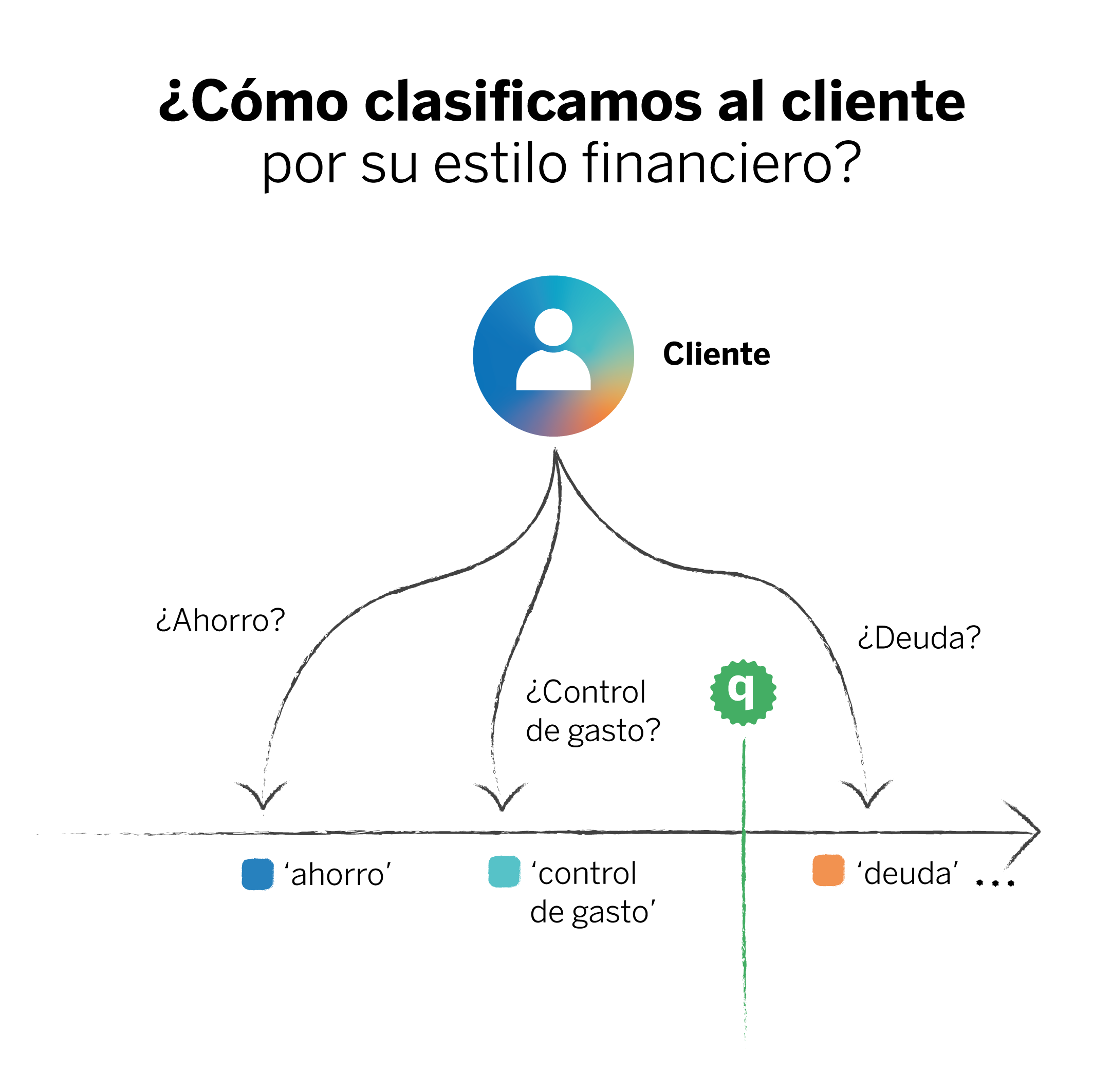
En este sentido, la incertidumbre reside en la elección de una de las dos categorías para ese cliente, pero evitamos que se le asocie con una categoría y no con otra. Esto podría derivar en la inclusión de nuevas recomendaciones financieras que quizá no habíamos previsto. El resultado es un clasificador mucho más fiable, donde la certeza de la predicción está garantizada, y donde podemos ver con claridad el conjunto de clases que tiene más probabilidad de contener la predicción correcta.

La utilización de rangos predictivos representa un cambio de paradigma en cómo interactuamos con los modelos y cómo los interpretamos. En lugar de preguntarnos “¿qué ocurrirá?”, comenzamos a pensar “¿qué es probable que ocurra y qué tan seguros estamos de ello?” En campos en los que el coste de equivocarse es elevado este cambio es crucial.

Cuatro virtudes, un reto y un aviso

Existen otras técnicas para hacer predicciones con un determinado grado de confianza. Sin embargo, hoy queremos destacar las virtudes de la aplicación de conformal prediction, sin perder de vista lo que debe tenerse en cuenta cuando se aplica y el reto que supone.

✨ Primera virtud: Flexibilidad sin precedentes

Una de las principales ventajas de esta técnica es su naturaleza libre de distribución. Esto significa que, a diferencia de los enfoques bayesianos y otros métodos estadísticos que requieren suposiciones específicas sobre la distribución de los datos (por ejemplo, que los datos sigan una distribución normal), conformal prediction no hace tales suposiciones. Esta flexibilidad la hace aplicable a un espectro más amplio de problemas, desde aquellos con distribuciones de datos bien entendidas hasta situaciones con datos altamente irregulares o poco comunes.

✨ Segunda virtud: Universalidad en su aplicación

Conformal prediction puede ser aplicada a cualquier modelo; es decir, es un método agnóstico. Desde una regresión lineal hasta redes neuronales profundas, esta técnica se puede utilizar indistintamente para cuantificar la incertidumbre de las predicciones. Esto permite a los científicos de datos utilizar sus modelos preferidos o los que sean más adecuados para la tarea en cuestión.

✨ Tercera virtud: Confianza en las predicciones

Su capacidad para proporcionar garantías de cobertura es, sin duda, la característica más distintiva de esta técnica. Para una región de predicción dada, podemos especificar con un grado de confianza (por ejemplo, 95%) que la región contendrá el resultado verdadero. Esta certeza probabilística nos ofrece una forma tangible de evaluar y comunicar la confianza en nuestras predicciones, facilitando la toma de decisiones informadas y la planificación de escenarios futuros.

✨ Cuarta virtud: Adaptabilidad

Esta técnica ajusta dinámicamente el tamaño de su conjunto de predicciones en función de la complejidad del ejemplo analizado. En situaciones donde los datos presentan patrones claros y son relativamente fáciles de predecir, conformal prediction ofrece conjuntos de predicción más pequeños. Por el contrario, ante ejemplos complicados donde la incertidumbre es significativamente mayor, los conjuntos de predicción se expanden.

⛰️ El reto: El dato de calibración

En el contexto de conformal prediction, una calibración precisa es esencial para asegurar que los intervalos de predicción tengan las propiedades de cobertura adecuadas. El modelo debe ser capaz de ajustar sus predicciones para capturar la verdadera distribución de los datos, reflejando adecuadamente el nivel de incertidumbre asociado con cada predicción.

Pero, diferentes conjuntos de datos y situaciones requieren distintos niveles de ajuste y enfoques de calibración. Un modelo puede funcionar bien y estar correctamente calibrado en un conjunto de datos, pero puede requerir ajustes significativos para mantener su precisión en otro. Esto implica que debemos tener un profundo entendimiento de la naturaleza de los datos, así como la habilidad para aplicar técnicas de calibración que puedan adaptarse con dinamismo a variaciones en los datos.

Abordar este desafío requiere una evaluación continua y rigurosa del rendimiento del modelo. Una buena calibración es un desafío técnico, pero también una herramienta de transparencia para ofrecer predicciones confiables y de calidad.

⚠️ Un aviso: Supuesto de intercambiabilidad

Este supuesto sostiene que los datos utilizados para el calibrado del modelo pueden ser intercambiados sin afectar las probabilidades. En muchos casos este supuesto aplica; pero, en situaciones donde los datos tienen una estructura temporal o espacial que quebranta la intercambiabilidad, es necesario adaptar o complementar conformal prediction con otros enfoques para mantener la fiabilidad de las predicciones.

¿Cómo se implementa Conformal Prediction?

Aunque existen diferentes algoritmos que mejoran la idea original de conformal prediction, el método general es común a todos ellos, al menos en su mayor parte. A continuación veremos cómo funciona para un caso general de clasificación. Recordemos que estos modelos nos indican la probabilidad de que el dato que deseamos clasificar (ya sea una imagen, un vector u otro tipo de entrada) pertenezca a cada una de las categorías disponibles. En otras palabras, estos modelos estiman en qué medida una entrada se ajusta a cada categoría.

Paso 0

Antes de entrenar nuestro modelo debemos separar un subconjunto de datos para la calibración, que no utilizaremos durante el entrenamiento ni la validación. Típicamente se dividen los datos de entrada en una proporción 80% | 20%, por lo que en este nuevo escenario de conformal prediction, podemos dividirlos en una proporción de, por ejemplo, 80% | 10% | 10%.

Paso 1

A continuación, nos aseguramos de entrenar y validar el modelo. Para ello, utilizamos los datos de entrenamiento y test. Recorremos entonces los datos de calibración y obtenemos la predicción de nuestro modelo para cada elemento (clase). De entre todas las probabilidades obtenidas para cada predicción, nos quedamos con la probabilidad asociada a la respuesta verdadera, además de la categoría o clase que representa.

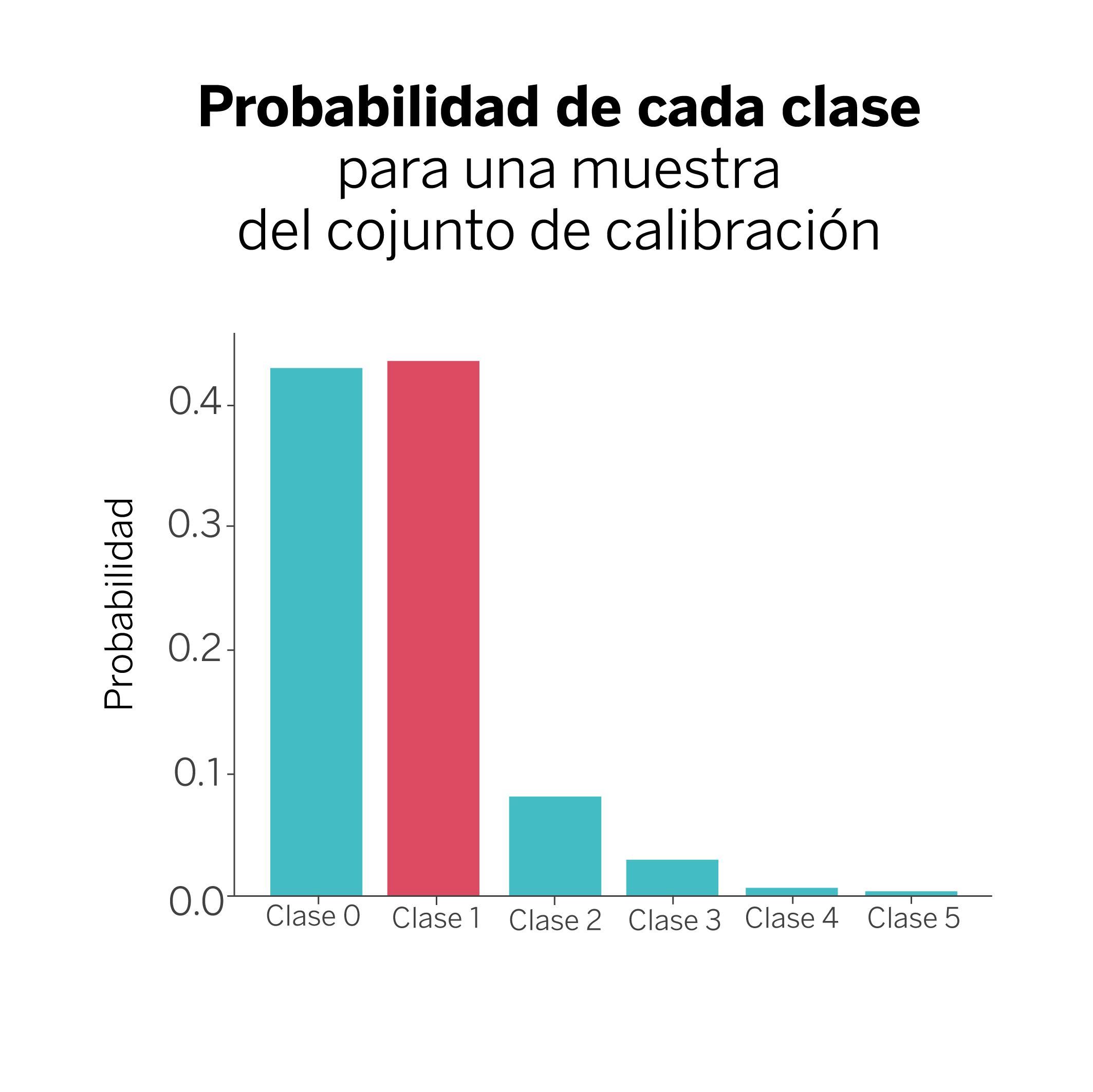
En nuestro ejemplo, disponemos de seis posibles categorías entre las que clasificar cada muestra. El modelo nos dice entonces que la respuesta verdadera en este caso es la clase #1, que típicamente se corresponderá con la probabilidad más alta, aunque no necesariamente. Podremos encontrar casos en los que la probabilidad asociada a la respuesta verdadera no sea la probabilidad más alta, pero esto no importa. En cualquier caso, lo que haremos será guardarnos la clase verdadera y la probabilidad asociada ({clase 1: 0.44}) para todos los ejemplos contenidos en el conjunto de calibración.

Paso 2

Calculamos el percentil 0.1 (10%) de todos los valores de probabilidad obtenidos en el paso anterior. En nuestro caso, ese valor es 0.42, y lo llamaremos q.

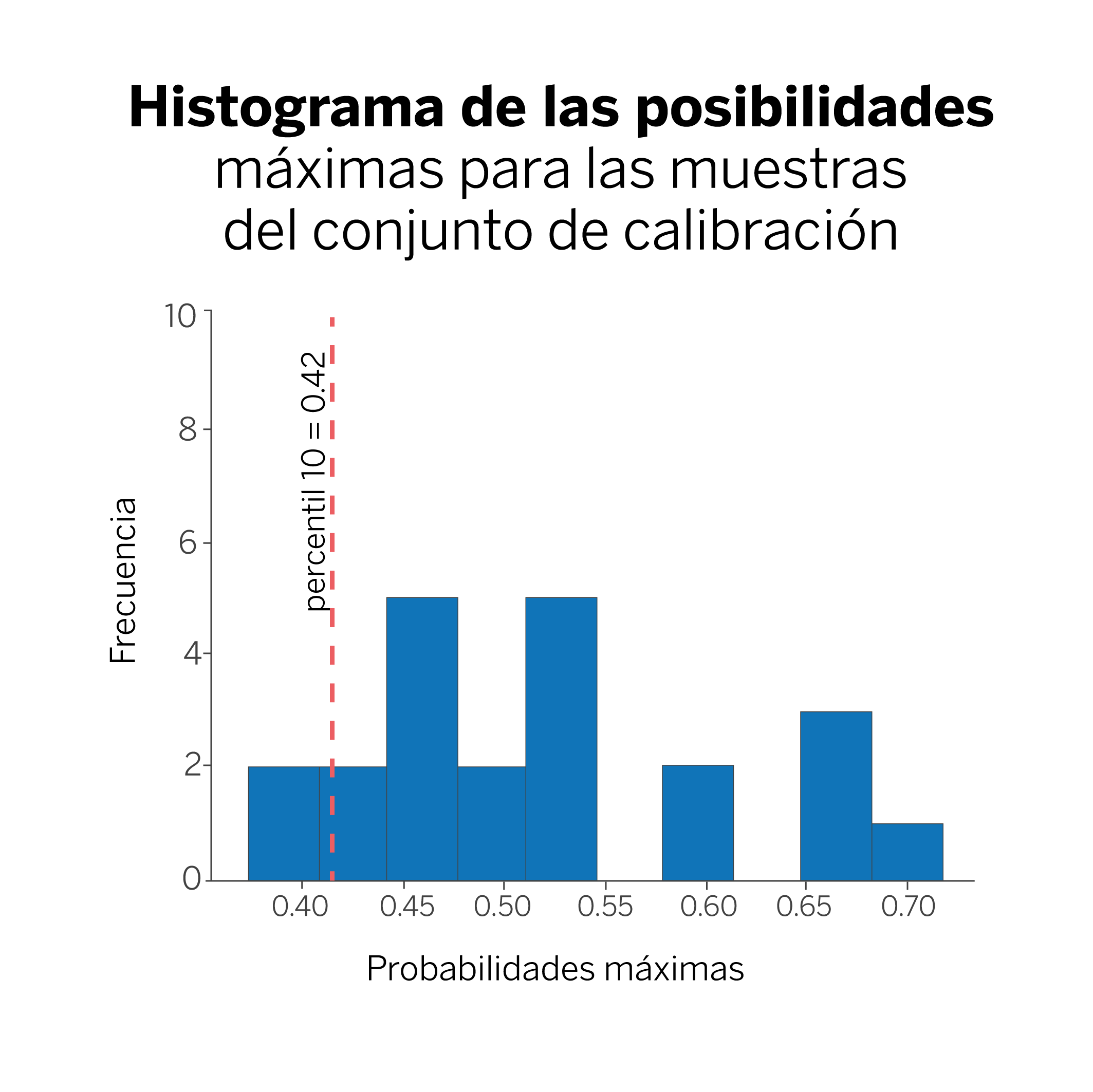
En esta figura, la línea que marca el percentil 10 nos indica que estamos seguros al 90% de que nuestro modelo clasifique una nueva muestra con una probabilidad mayor que 0.42 ¿Por qué el 90%? Porque hemos elegido el percentil 10. Si hubiéramos elegido calcular el percentil 5, entonces nuestra cobertura sería del 95%.

Paso 3

Ya estamos preparados para realizar predicciones usando conformal prediction. Cuando vayamos a clasificar una nueva muestra, lo único que tenemos que hacer es pedirle a nuestro modelo las probabilidades asignadas a cada posible clase a la que puede pertenecer, y seleccionar únicamente aquellas con un valor mayor que el valor calculado para “q”.

En el ejemplo, podemos ver que las probabilidades para las clases “0” y “1” están por encima del umbral “q”. En este caso, en lugar de dar como predicción la clase “1”, diremos que la muestra pertenece al conjunto {“clase 0”, “clase 1”}; es decir, a alguna de estas dos clases, con una probabilidad del 90%.

Incertidumbre sí, pero rigurosa

Tener un conocimiento riguroso de la incertidumbre es una manera de hacernos fuertes ante la naturaleza incierta de las predicciones. Gracias a este conocimiento, disponemos de la información necesaria para tomar decisiones fundamentadas.

Hoy en día, el dilema de Creso puede interpretarse como una metáfora sobre la ambigüedad de las predicciones que se hacen en forma de afirmación rotunda: hay que matizarlas y barajar con cautela las posibilidades reales. Con herramientas como conformal prediction, la cual tiene una fina sensibilidad hacia la naturaleza dinámica de los datos, podemos confiar en que nuestras decisiones cotidianas son, efectivamente, las más acertadas.